Сумма векторов - это фундаментальная операция в векторной алгебре, представляющая собой сложение двух или более векторов по определенным правилам. Результатом сложения является новый вектор, называемый векторной суммой.
Содержание
Основные способы сложения векторов
| Метод | Описание |
| Правило треугольника | Векторы откладываются последовательно друг за другом |
| Правило параллелограмма | Векторы откладываются из одной начальной точки |
| Координатный метод | Сложение соответствующих координат векторов |
Геометрическая интерпретация
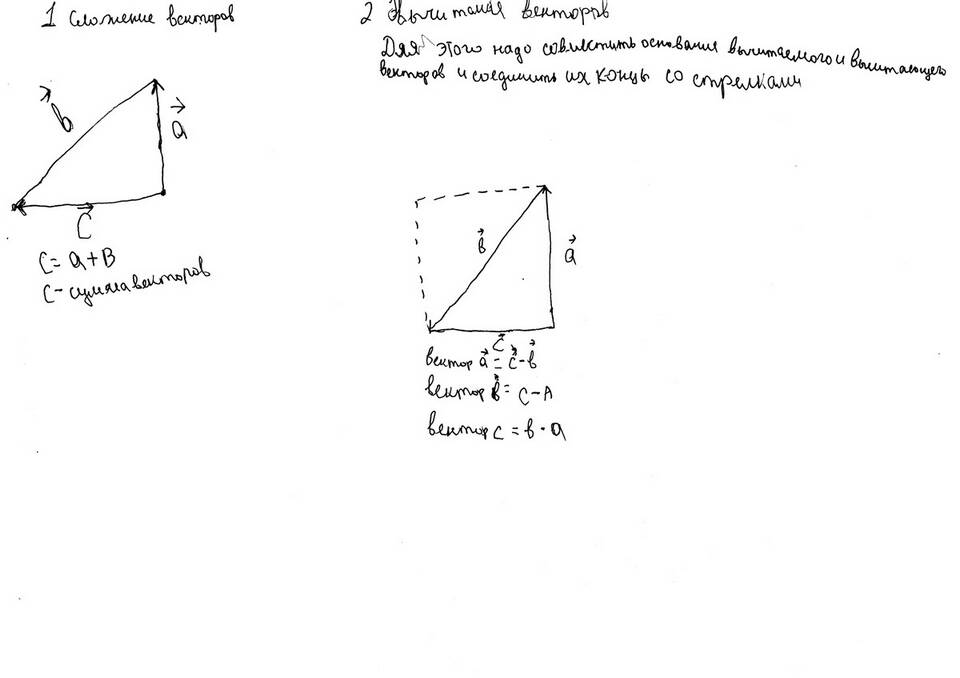
Сумма векторов a и b - это вектор c, который можно получить:
- Отложив вектор b от конца вектора a (правило треугольника)
- Построив параллелограмм на векторах a и b (правило параллелограмма)
Алгебраические свойства суммы векторов
Основные свойства
- Коммутативность: a + b = b + a
- Ассоциативность: (a + b) + c = a + (b + c)
- Существование нулевого вектора: a + 0 = a
- Существование противоположного вектора: a + (-a) = 0
Координатное представление
Для векторов в декартовой системе координат:
| Вектор a | (x₁, y₁, z₁) |
| Вектор b | (x₂, y₂, z₂) |
| Сумма a + b | (x₁+x₂, y₁+y₂, z₁+z₂) |
Применение суммы векторов
- Физика: сложение сил, скоростей, ускорений
- Компьютерная графика: перемещение объектов
- Навигация: расчет результирующего направления
- Экономика: анализ многомерных данных
Примеры вычисления суммы
| Пример | Решение |
| a = (2, 3), b = (1, -1) | a + b = (3, 2) |
| a = (0, 5), b = (-2, 3) | a + b = (-2, 8) |
| a = (1, 1, 1), b = (2, 3, 4) | a + b = (3, 4, 5) |
Особые случаи
- Сумма коллинеарных векторов - вектор того же направления
- Сумма перпендикулярных векторов - диагональ прямоугольника
- Сумма противоположных векторов - нулевой вектор